|
3.已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求: (1)当市场商品价格为P=100时,厂商实现MR=LMC时的产量、平均成本和利润;(4分) (1)根据题意,有: LMC= 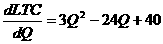 且完全竞争厂商的P=MR,根据已知条件P=100,故有MR=100。 由利润最大化的原则MR=LMC,得:3Q2-24Q+40=100 整理得 Q2-8Q-20=0 解得Q=10(负值舍去了) 又因为平均成本函数SAC(Q)= 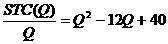 所以,以Q=10代入上式,得: 平均成本值SAC=102-12×10+40=20 最后,利润=TR-STC=PQ-STC =(100×10)-(103-12×102+40×10)=1000-200=800 因此,当市场价格P=100时,厂商实现MR=LMC时的产量Q=10,平均成本SAC=20,利润为 л=800。 (2)该行业长期均衡时的价格和单个厂商的产量;(4分) (2)由已知的LTC函数,可得: LAC(Q)= 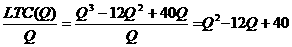 令 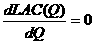 ,即有: ,即有: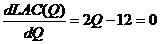 ,解得Q=6 ,解得Q=6且 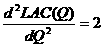 >0 >0解得Q=6 所以Q=6是长期平均成本最小化的解。 以Q=6代入LAC(Q),得平均成本的最小值为: LAC=62-12×6+40=4 由于完全竞争行业长期均衡时的价格等于厂商的最小的长期平均成本,所以,该行业长期均衡时的价格P=4,单个厂商的产量Q=6。 (3)当市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。(4分) (3)由于完全竞争的成本不变行业的长期供给曲线是一条水平线,且相应的市场长期均衡价格是固定的,它等于单个厂商的最低的长期平均成本,所以,本题的市场的长期均衡价格固定为P=4。以P=4代入市场需求函数Q=660-15P,便可以得到市场的长期均衡数量为Q=660-15×4=600。 4.假设货币需求为L=0.2y-10r,货币供给为200美元,c=60+0.8y,t=100,i =150,g=100。(18分) (1) 求IS和LM方程;(4分) (1)IS:150+100= -60+0.2(y – 100)+100 (1) y=1150(1) LM:0.2y-10r= 200(1) y=1000+50r(2) (2) 求均衡收入、利率和投资;(4分) 均衡时IS=LM 即1150=1000+50r 所以均衡时 r=3 y=1150 i=150 |




